今回は「奥深い確率論のお話！」シリーズラストで、1回目からお伝えしてきた

確率問題の結論の根拠をお伝えします。

「奥深い確率論のお話！2/3」でお伝えいたしましたが、

今回のこの問題、結論的には「もう一方のドアに変更したほうが確率は上がる」というのが

数学的に正しいようです。

ちなみに、モンティからハズレのヤギのドアを開けて見せてもらった後、残りの2つのドアを選ぶ際に

例えばプレーヤーがコイントスでドアを決めたとすれば、確立は1/2になります。

しかし、「奥深い確率論のお話！1/3と2/3」でお伝えしたルールに基づいて決めた場合は、

変更したほうが確率が上がるのです。

では、なぜ確率は上がるのでしょうか？？

根拠をお伝えいたします！！

プレーヤーが初めに選んだドアをA、残りのドアをB、Cとする。プレーヤーが初めのドアを選んだ時点で、

それぞれのドアに景品がある確率と、モンティがそれぞれのドアを開ける確率を表にすると以下のようになります。

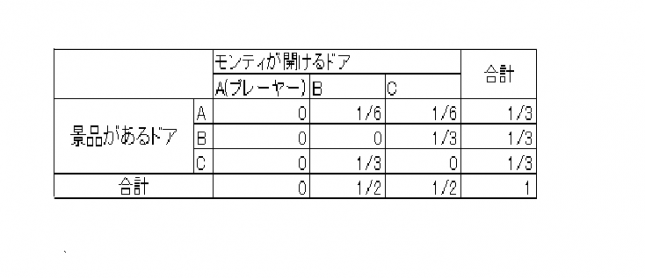
仮にAに景品がある場合、まず景品があるドアがAである確率は1/3です。

プレーヤーはAのドアを最初に選択しており、且つモンティは

はずれのヤギがいるドアを開けるため、モンティがAのドアを開ける確率は 0 になります。

次にモンティがBのドアを開ける確率を考えると、Aに景品がある確率の1/3にB及びCの2つのドアから

Bを選ぶ確率の1/2を掛けた1/6となります。

モンティがこの時、Cのドアを選んで開ける確率も同様に1/6です。

次にBに景品がある場合の確率を見てみましょう。プレーヤーはAを選択しており、景品はBにあるので、

モンティはCのドアを開ける選択肢しかありません。

そのCのドアを開ける確率は、景品がBにある確立と等しくなるため、1/3です。

景品の新車がCにある時も同様に、モンティはBのドアを開く選択肢しか無いため、確率は1/3です。

ここで考えて見ましょう。

プレーヤーがAのドアを選択しており、モンティがBのドアを開けた場合、景品がAにある確立より

Cにある確立のほうが高いことが表から分かります。

(景品がAにある時にBを開ける確率=1/6　＜　景品がCにある時にBを開ける確率=1/3)

よってプレーヤーはAからCのドアに変更するべきだと言えるのです。

別の解説をしますと、最初にプレーヤーが当りのドアを選ぶ確率は1/3で、はずれのドアを選ぶ確率は2/3です。

最初に当りのドアを選んだ後、第二のドアで当たる確率は０で、はずれのドアを選んだ後、

第二のドアで当たる確率は100%です。

(最初に選んだドア以外の2つのドア【2/3】のうちはずれの1つをモンティが開けるため、残り1つのドアに確率が集約する。)

つまり、

第2のドアで当たる確率は 1/3×0 + 2/3×1 = 2/3

同様にして、

最初のドアで当たる確率 = 1/3×1 + 2/3×0 = 1/3

上記計算式より、第2のドアに替えた場合、最初に当たりだとハズレになり、逆にハズレだと当たりになります。

つまり、最初のドアを選ぶときは「当たり、ハズレ、ハズレ」の組み合わせだったものが、

第2のドアを選ぶときには「ハズレ、当たり、当たり」のドアになることが分かります。

よって、第2のドアを選ぶときは「当たり」と「ハズレ」の確率が完全に逆転するのです。

結果的に、

最初のドアでは「ハズレ」の方が多いので、当然「当たり」の方が多くなる第2のドアを選択すべき。　となるのです。

最初は1/3で当たりだったものが、2/3で当たりになるので、

この問題の答えは「ドアを選びなおすべき！」となります。

なかなか納得しがたい論理だったのではないでしょうか？？

ポイントは、最初に示したルールを守っていることです。

これに似た問題で「3囚人問題」というのもありますので、是非調べてみてはいかがでしょうか。